
In addition, the peak fitting includes the various profile coefficients thus fully describing the instrument contribution to the peak profiles. Relief of stresses results in vacancies or micropores, which coalesce into voids upon heat treatment. The positions are compared to those expected from the known lattice parameters to establish the diffractometer constants (difC, difA, difB and Zero) used for calculating TOF peak positions from d-spacings. Micropore formation is explained by differential shrinkage of the various crystalline fractions formed during solidification, giving rise to internal stresses in the solid alloy. Alloys quenched from the liquid state do not show any microporosity the voids appear after homogenization at 800☌. The phase represents a substitutional solid solution without structural defects. Upon cold rolling the voids close and the differences disappear. For this example, the molecular dynamics simulation calculates the equilibrium lattice constant and the corresponding cohesive energy for aluminum. With the increase of In content the experimental densities become increasingly lower than the calculated ones because of void formation. The thermal expansion coefficients between 15 and 65☌ of the homogeneous alloys increase from 14.87 (pure Cu) to 17.2 × 10-6☌-1 at the solid solubility limit (10.4 atomic % In, quenched from 650☌). The angles between these sides, which are typically labeled, , and. A simple cubic crystal has only one lattice constant, the distance between atoms, but in general lattices in three dimensions. The typical lattice parameters that are used are the length of each side, which are typically labeled a, b, and c, which are known as lattice constants. In the solid solution region additions of In increase the lattice parameter of Cu according to ax = 3.6149 + 0.0091x up to x = 10.4 (x = atomic % In, balance Cu). A lattice constant or lattice parameter is one of the physical dimensions and angles that determine the geometry of the unit cells in a crystal lattice, and is proportional to the distance between atoms in the crystal.
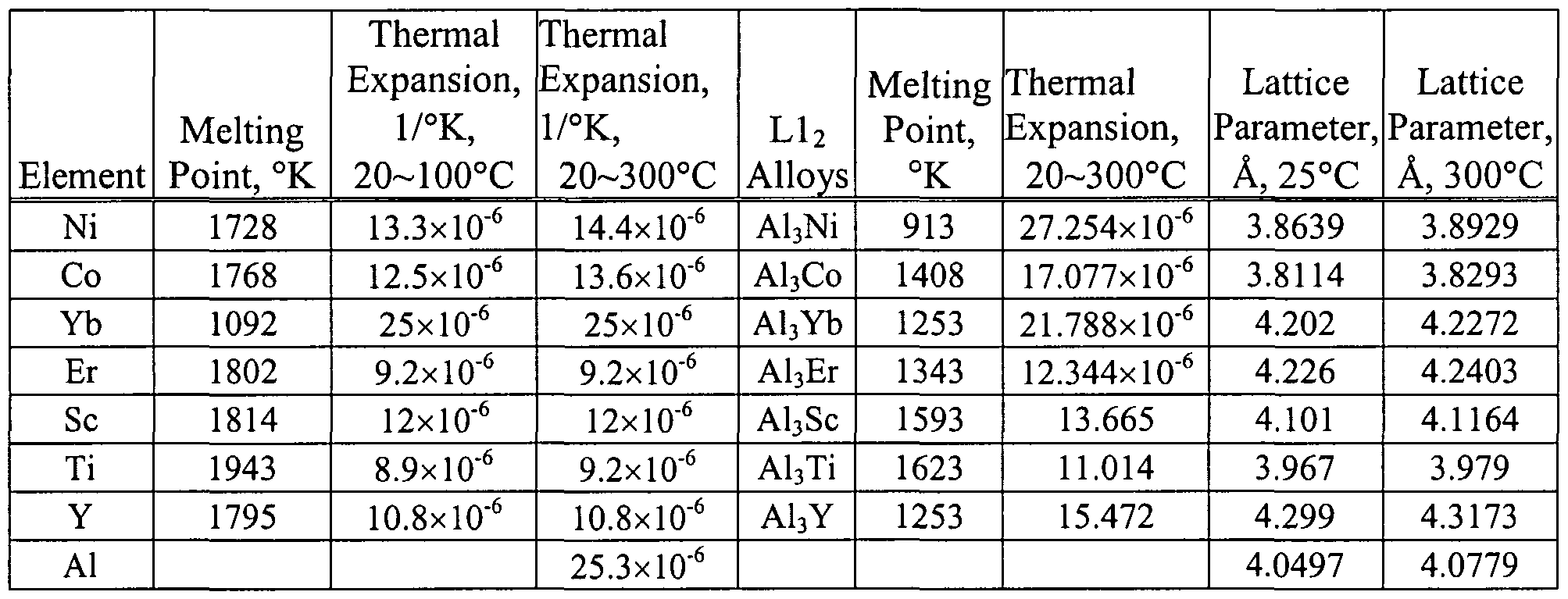
Table E.1 Lattices of elemental single crystals. The measured density d25 is 8.9314 ± 0.0002 g.cm-3 in agreement with the calculated value dx = 8.9316. ing lattice parameters of elemental crystals. Spectroscopically pure Cu has a lattice parameter a25 = 3.61491 Å (corrected for refraction), and a thermal expansion coefficient = 14.87 × 10-6☌-1 between 15 and 55☌.


 0 kommentar(er)
0 kommentar(er)
